1 Linear Systems Matrices Pdf System Of Linear Equations Matrix Mathematics

Matrices And System Of Linear Equations PDF | PDF | Determinant | Matrix (Mathematics)

Matrices And System Of Linear Equations PDF | PDF | Determinant | Matrix (Mathematics) This handout will focus on how to solve a system of linear equations using matrices. matrices are useful for solving systems of equations. there are two main methods of solving systems of equations: gaussian elimination and gauss jordan elimination. both processes begin the same way. Augmented matrix: a matrix used to represent a system of equations. it consist of the coefficient matrix with an extra column on the far right with the solutions.

MATRICES-AND-SYSTEMS-OF-LINEAR-EQUATIONS_Part-1_Feb14 | PDF | System Of Linear Equations ...

MATRICES-AND-SYSTEMS-OF-LINEAR-EQUATIONS_Part-1_Feb14 | PDF | System Of Linear Equations ... This topic introduces the gauss and gauss jordan methods. for convenience, the examples and exercises in this module use small systems of equations, however the methods are applicable to systems of any size. Ices associated to a linear system. matrix algebra is a fascinating subject with numerous applications in every branch of engineering, medicine, statistics, mathematics. Characterize a linear system in terms of the number of solutions, and whether the system is consistent or inconsistent. apply elementary row operations to solve linear systems of equations. express a set of linear equations as an augmented matrix. Note: 1) for a non homogeneous linear equations system ax=b, if |a|≠0, then a unique solution exists; 2) otherwise, i.e. |a|=0, the matrix is singular. 2) for a homogeneous linear equations system ax=0, if |a|=0 and if it has non trivial solution (x=0), which will be discussed later in this course.

Chapter 1. Systems Of Linear Equations | PDF | System Of Linear Equations | Matrix (Mathematics)

Chapter 1. Systems Of Linear Equations | PDF | System Of Linear Equations | Matrix (Mathematics) Characterize a linear system in terms of the number of solutions, and whether the system is consistent or inconsistent. apply elementary row operations to solve linear systems of equations. express a set of linear equations as an augmented matrix. Note: 1) for a non homogeneous linear equations system ax=b, if |a|≠0, then a unique solution exists; 2) otherwise, i.e. |a|=0, the matrix is singular. 2) for a homogeneous linear equations system ax=0, if |a|=0 and if it has non trivial solution (x=0), which will be discussed later in this course. We now come to one of the most important use of matrices, that is, using matrices to solve systems of linear equations. we showed informally, in example 1 of sec. 7.1, how to represent the information contained in a system of linear equations by a matrix, called the augmented matrix. In this chapter we see that, in general, linear systems of equations are best represented in terms of matrices and that, once such a representation has been made, the set of all solutions to the system can be easily determined. A list (s1; s2; :::; sn) of numbers that makes each equation in the system true when the values s1; s2; :::; sn are substituted for x1; x2; :::; xn, respectively. To solve a system of linear equations by using gaussian elimination to bring the augmented matrix into row echelon form without continuing all the way to the reduced row echelon form.

Solution Of Systems Of Linear Equations | PDF | System Of Linear Equations | Matrix (Mathematics)

Solution Of Systems Of Linear Equations | PDF | System Of Linear Equations | Matrix (Mathematics) We now come to one of the most important use of matrices, that is, using matrices to solve systems of linear equations. we showed informally, in example 1 of sec. 7.1, how to represent the information contained in a system of linear equations by a matrix, called the augmented matrix. In this chapter we see that, in general, linear systems of equations are best represented in terms of matrices and that, once such a representation has been made, the set of all solutions to the system can be easily determined. A list (s1; s2; :::; sn) of numbers that makes each equation in the system true when the values s1; s2; :::; sn are substituted for x1; x2; :::; xn, respectively. To solve a system of linear equations by using gaussian elimination to bring the augmented matrix into row echelon form without continuing all the way to the reduced row echelon form.

Linear Algebra Fundamentals: Solutions Of Linear Systems, Determinants, And Matrix Inversion ...

Linear Algebra Fundamentals: Solutions Of Linear Systems, Determinants, And Matrix Inversion ... A list (s1; s2; :::; sn) of numbers that makes each equation in the system true when the values s1; s2; :::; sn are substituted for x1; x2; :::; xn, respectively. To solve a system of linear equations by using gaussian elimination to bring the augmented matrix into row echelon form without continuing all the way to the reduced row echelon form.

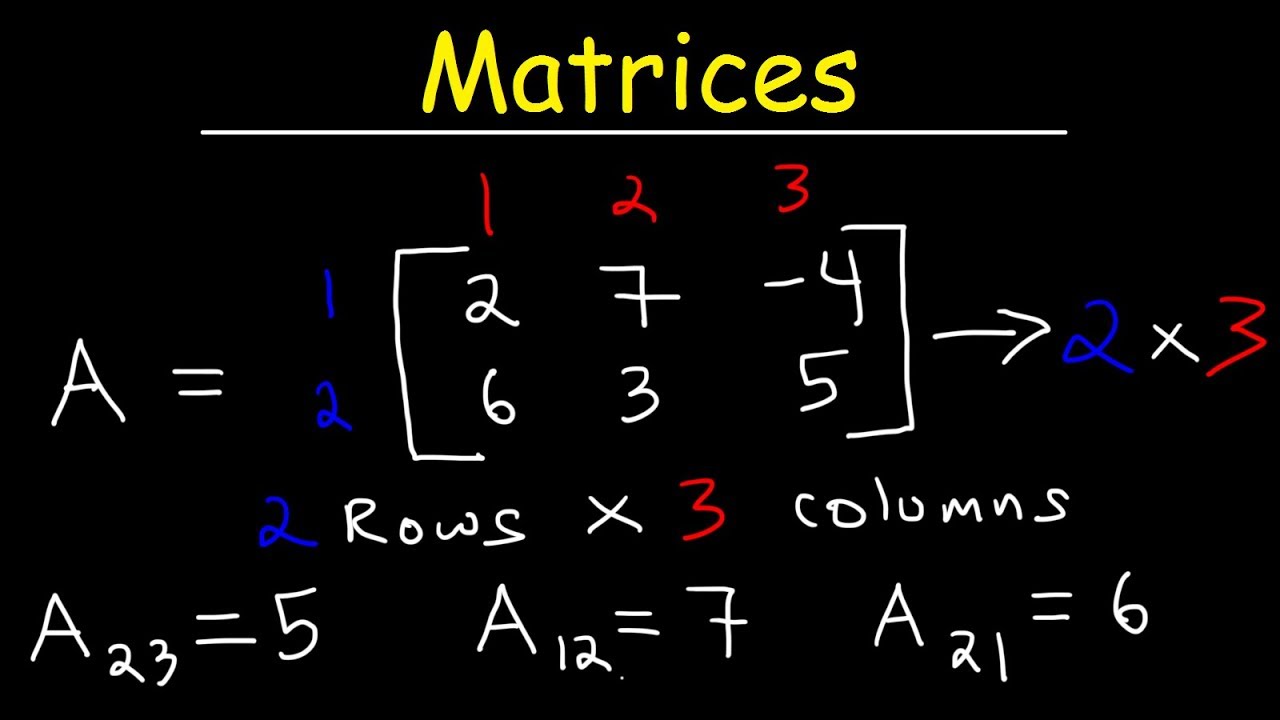
Intro to Matrices