Complex Analysis L04 The Complex Logarithm Logz

7_Logarithm Of Complex Number | Download Free PDF | Complex Number | Logarithm

7_Logarithm Of Complex Number | Download Free PDF | Complex Number | Logarithm This video introduces the complex logarithm, log (z), as the inverse of the complex exponential. the logarithm is a very important function that has infinitely many values in the complex. We can visualize the multiple valued nature of log z by using riemann surfaces. the following interactive images show the real and imaginary components of log (z).

Logarithm 1 | PDF | Logarithm | Complex Analysis

Logarithm 1 | PDF | Logarithm | Complex Analysis Explore the complex logarithm, log (z), in this 28 minute video lecture on complex analysis. delve into the inverse of the complex exponential and understand its significance as a function with infinitely many values in the complex plane. 5.2 the complex logarithm in section 5.1, we showed that, if w is a nonzero complex number, then the equation w = exp z has infinitely many solutions. because the function exp (z) is a many to one function, its inverse (the logarithm) is necessarily multivalued. Before using the chain rule, how do you know that lnz is differentiable? point (c) here asks to do something to calculate $\; (\log z)'\;$ , from which i deduce it already is given. besides this, being the inverse of a differentiable function it is differentiable, too. Our goal in this section is to define the log function. we want log (z) to be the inverse of exp (z) . that is, we want exp (log (z))=z . we will see that log (z) is multiple valued, so when we use ….

Complex Analysis: The Complex Logarithm Worksheet For Higher Ed | Lesson Planet

Complex Analysis: The Complex Logarithm Worksheet For Higher Ed | Lesson Planet Before using the chain rule, how do you know that lnz is differentiable? point (c) here asks to do something to calculate $\; (\log z)'\;$ , from which i deduce it already is given. besides this, being the inverse of a differentiable function it is differentiable, too. Our goal in this section is to define the log function. we want log (z) to be the inverse of exp (z) . that is, we want exp (log (z))=z . we will see that log (z) is multiple valued, so when we use …. We shall return to the murky world of branch cuts as we expand our repertoire of complex functions when we encounter the complex logarithm function. define w = log z as the inverse of z = ew. your textbook (zill & shanahan) uses ln instead of log and ln instead of log . We use ln only for logarithms of real numbers; log denotes logarithms of com plex numbers using base e (and no other base is used). because equation 3.21 yields logarithms of every nonzero complex number, we have defined the complex logarithm function. The principal value of log is characterised by log 1 = 0. instead of removing the negative real numbers, we could have removed any path from 0 whose complement is simply connected. Since z →log|z| is clearly continuous for all z ∈ c \{0} and since logz =log|z| iarg(z), the result follows from the fact that z →arg(z) is discontinuous at each point on the nonpositive real axis.

07 - Complex Numbers - Logarithms Of Complex Numbers | PDF | Complex Number | Logarithm

07 - Complex Numbers - Logarithms Of Complex Numbers | PDF | Complex Number | Logarithm We shall return to the murky world of branch cuts as we expand our repertoire of complex functions when we encounter the complex logarithm function. define w = log z as the inverse of z = ew. your textbook (zill & shanahan) uses ln instead of log and ln instead of log . We use ln only for logarithms of real numbers; log denotes logarithms of com plex numbers using base e (and no other base is used). because equation 3.21 yields logarithms of every nonzero complex number, we have defined the complex logarithm function. The principal value of log is characterised by log 1 = 0. instead of removing the negative real numbers, we could have removed any path from 0 whose complement is simply connected. Since z →log|z| is clearly continuous for all z ∈ c \{0} and since logz =log|z| iarg(z), the result follows from the fact that z →arg(z) is discontinuous at each point on the nonpositive real axis.

Complex Logarithm - Equations, Properties, And Examples

Complex Logarithm - Equations, Properties, And Examples The principal value of log is characterised by log 1 = 0. instead of removing the negative real numbers, we could have removed any path from 0 whose complement is simply connected. Since z →log|z| is clearly continuous for all z ∈ c \{0} and since logz =log|z| iarg(z), the result follows from the fact that z →arg(z) is discontinuous at each point on the nonpositive real axis.

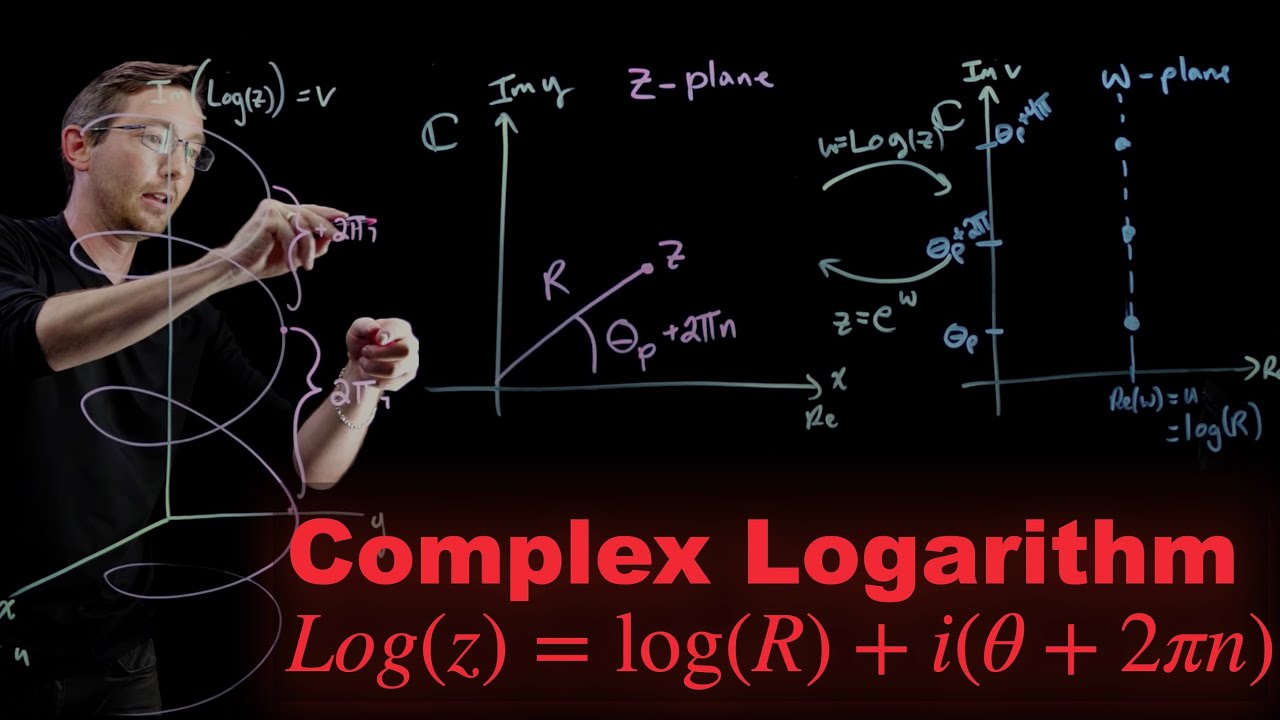
Complex Analysis L04: The Complex Logarithm, Log(z)