Complex Number Theory Pdf Circle Complex Number

Complex Number Theory | PDF | Circle | Complex Number

Complex Number Theory | PDF | Circle | Complex Number The geometrical representation of complex numbers can be very useful when complex number methods are used to investigate properties of triangles and circles. it is very important in the branch of calculus known as complex function theory, where geometric methods play an important role. We can represent complex numbers graphically on a x–y coordinate system where point (a, b) represents the complex number a bi. we call this the rectangular form of complex numbers.

Complex Numbers, Theory (1) | PDF | Complex Number | Circle

Complex Numbers, Theory (1) | PDF | Complex Number | Circle Complex numbers on the unit circle inates of the form (cos j, sin j). here, j is the angle from the positive x axis to the radius vector, the vector pointing from the ori gin to the given point. This gives us the sense that a complex number z can be represented as the point (a; b) in the complex plane, with the horizontal axis representing the real part and the vertical axis representing the imaginary part. The third chapter is dedicated to the geometry of circle and triangle on the base of complex numbers. numerous theorems are proposed, namely: menelau’s theorem, pascal’s and desargue’s theorem, ceva’s and van aubel’s theorem, stewart’s theorem, ptolemy’s theorem and others. This document is a comprehensive chapter on complex numbers, covering topics such as imaginary numbers, algebraic operations, representation in the complex plane, and various properties and theorems related to complex numbers.

Complex Number | PDF

Complex Number | PDF The third chapter is dedicated to the geometry of circle and triangle on the base of complex numbers. numerous theorems are proposed, namely: menelau’s theorem, pascal’s and desargue’s theorem, ceva’s and van aubel’s theorem, stewart’s theorem, ptolemy’s theorem and others. This document is a comprehensive chapter on complex numbers, covering topics such as imaginary numbers, algebraic operations, representation in the complex plane, and various properties and theorems related to complex numbers. Swiss born mathematician jean robert argand, after a systematic study on complex numbers, represented every complex number as a set of ordered pair (x,y) on a plane called complex plane. Multiplication with a real number corresponds to stretching, so we conclude from the above that multiplication with a complex number corresponds to a rotation and stretching of the plane. Expressing a complex number z in cartesian coordinates as x iy (where x and y are real numbers), we call x the real part of z and y the imaginary part of z, and write x = re z and y = im z. Where a; b are real, is the sum of a real and an imaginary number. the real part of z=a bi: refzg = a is a real number. the imaginary part of z=a bi: imfzg = b is a also a real number. a complex number z=a bi represents a point (a; b) in a 2d space, called the complex plane. im{z} z=a bi.

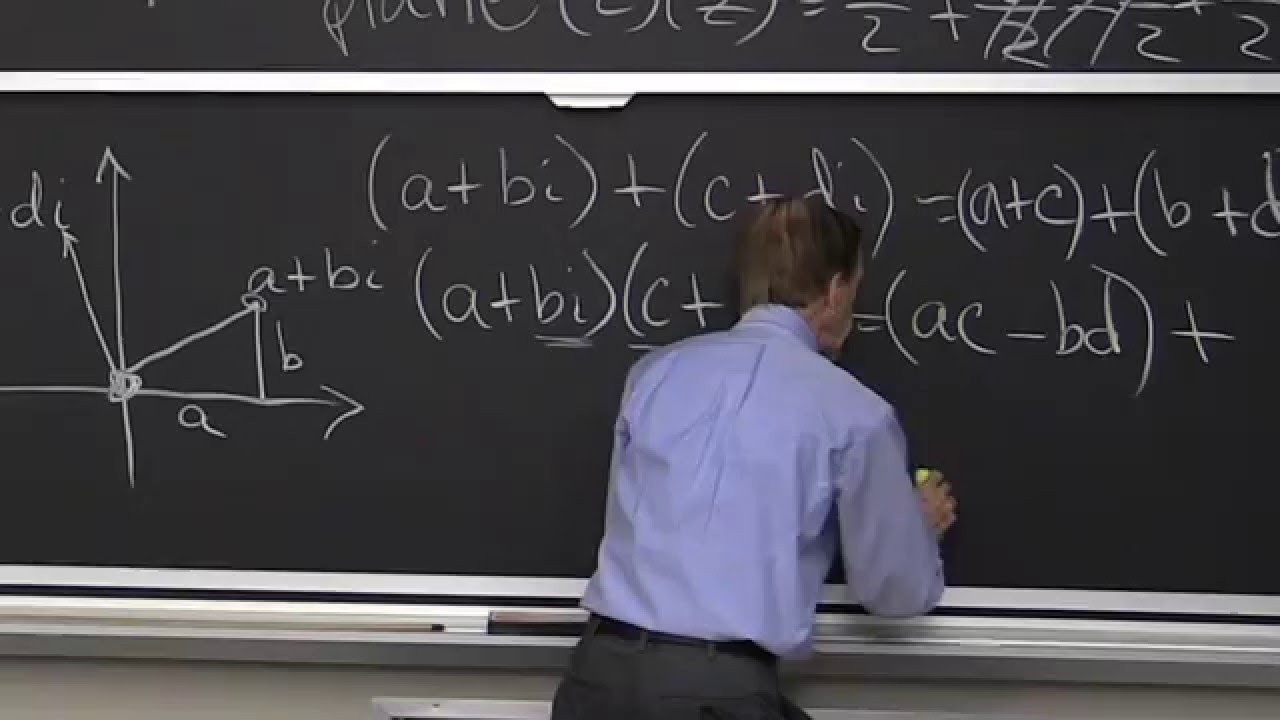
Complex Numbers: Part Imaginary, but Really Simple