Evaluate Functions Khan Academy Youtube

Evaluate Functions From Their Graph Algebra (practice) Khan Academy | PDF

Evaluate Functions From Their Graph Algebra (practice) Khan Academy | PDF Examples & evidence for example, if you wanted to evaluate more sums like this, you would use the same process: combine numbers in pairs and keep a running total, adjusting as needed when subtracting. this solution follows basic arithmetic rules and calculations can be verified using a calculator or arithmetic checks. For example, if we wanted to evaluate the expression for a different value of x, say x = 3, we would substitute and calculate: 21(8)3 = 21(512) = 256.

Evaluate Functions | PDF

Evaluate Functions | PDF To evaluate (−252)2, first convert the mixed number to an improper fraction, which gives − 512. squaring this leads to 25144, or as a mixed number, 52519. To evaluate the expression ∣ −31.889∣, we need to understand the concept of absolute value. the absolute value of a number is its distance from zero on the number line, disregarding whether the number is positive or negative. To evaluate (g ∘ f)(0), we first need to understand what this composite function means. the notation (g ∘ f)(x) represents the function g(f (x)). this means we will first apply the function f to an input, and then use the output of that function as the input for the function g. given the functions: f (x) = x1 g(x) = x − 4 we will now find f (0). however, when we calculate f (0): f (0. To evaluate (2− 5)(p q)(i) when p = 2 and q = 5, follow these steps: substitute the given values for p and q: p = 2 and q = 5 calculate the expression inside the parentheses: (p q) = (2 5) = 7 evaluate the expression (2− 5): 2 − 5 = −3 combine the results with the imaginary unit i: the expression now becomes (−3)(7)(i). compute the final result: (−3) ×7 = −21 therefore.

EVALUATING FUNCTIONS - YouTube

EVALUATING FUNCTIONS - YouTube To evaluate (g ∘ f)(0), we first need to understand what this composite function means. the notation (g ∘ f)(x) represents the function g(f (x)). this means we will first apply the function f to an input, and then use the output of that function as the input for the function g. given the functions: f (x) = x1 g(x) = x − 4 we will now find f (0). however, when we calculate f (0): f (0. To evaluate (2− 5)(p q)(i) when p = 2 and q = 5, follow these steps: substitute the given values for p and q: p = 2 and q = 5 calculate the expression inside the parentheses: (p q) = (2 5) = 7 evaluate the expression (2− 5): 2 − 5 = −3 combine the results with the imaginary unit i: the expression now becomes (−3)(7)(i). compute the final result: (−3) ×7 = −21 therefore. For a similar example, if we had f (x) = and g(x) = x 4 and we evaluated at x = 2, we would compute f (2) = 8 and g(2) = 6, giving us (f g)(2) = 14. 3 20 45 3 2 calculate inside the parentheses first: calculate 3 2: 3 2 = 5 so, the expression now looks like 3× 20 [45− 5]. then perform the subtraction in the brackets: calculate 45− 5: 45 − 5 = 40 now the expression simplifies to 3 × 20 40. now perform the multiplication: calculate 3× 20: 3 × 20 = 60 the expression now becomes 60 40. finally, do the addition: calculate 60. We are given the values x = 7 and y = 4, and we need to evaluate the expressions 12 x, 3x y, 4y − 10, and 21 xy. then, we need to match each expression to its corresponding value from the set {6, 14, 25, 19}. Let's evaluate the expression step by step: the expression we have is: 2(4 8)(6 −3). evaluate inside the parentheses: start by calculating 4 8, which equals 12. next, calculate 6− 3, which equals 3. multiply the results: now, take the result of the first parentheses, which is 12, and multiply it by the result of the second parentheses.

P1 4 Evaluating Functions - YouTube

P1 4 Evaluating Functions - YouTube For a similar example, if we had f (x) = and g(x) = x 4 and we evaluated at x = 2, we would compute f (2) = 8 and g(2) = 6, giving us (f g)(2) = 14. 3 20 45 3 2 calculate inside the parentheses first: calculate 3 2: 3 2 = 5 so, the expression now looks like 3× 20 [45− 5]. then perform the subtraction in the brackets: calculate 45− 5: 45 − 5 = 40 now the expression simplifies to 3 × 20 40. now perform the multiplication: calculate 3× 20: 3 × 20 = 60 the expression now becomes 60 40. finally, do the addition: calculate 60. We are given the values x = 7 and y = 4, and we need to evaluate the expressions 12 x, 3x y, 4y − 10, and 21 xy. then, we need to match each expression to its corresponding value from the set {6, 14, 25, 19}. Let's evaluate the expression step by step: the expression we have is: 2(4 8)(6 −3). evaluate inside the parentheses: start by calculating 4 8, which equals 12. next, calculate 6− 3, which equals 3. multiply the results: now, take the result of the first parentheses, which is 12, and multiply it by the result of the second parentheses.

Evaluate Functions : Khan Academy - YouTube

Evaluate Functions : Khan Academy - YouTube We are given the values x = 7 and y = 4, and we need to evaluate the expressions 12 x, 3x y, 4y − 10, and 21 xy. then, we need to match each expression to its corresponding value from the set {6, 14, 25, 19}. Let's evaluate the expression step by step: the expression we have is: 2(4 8)(6 −3). evaluate inside the parentheses: start by calculating 4 8, which equals 12. next, calculate 6− 3, which equals 3. multiply the results: now, take the result of the first parentheses, which is 12, and multiply it by the result of the second parentheses.

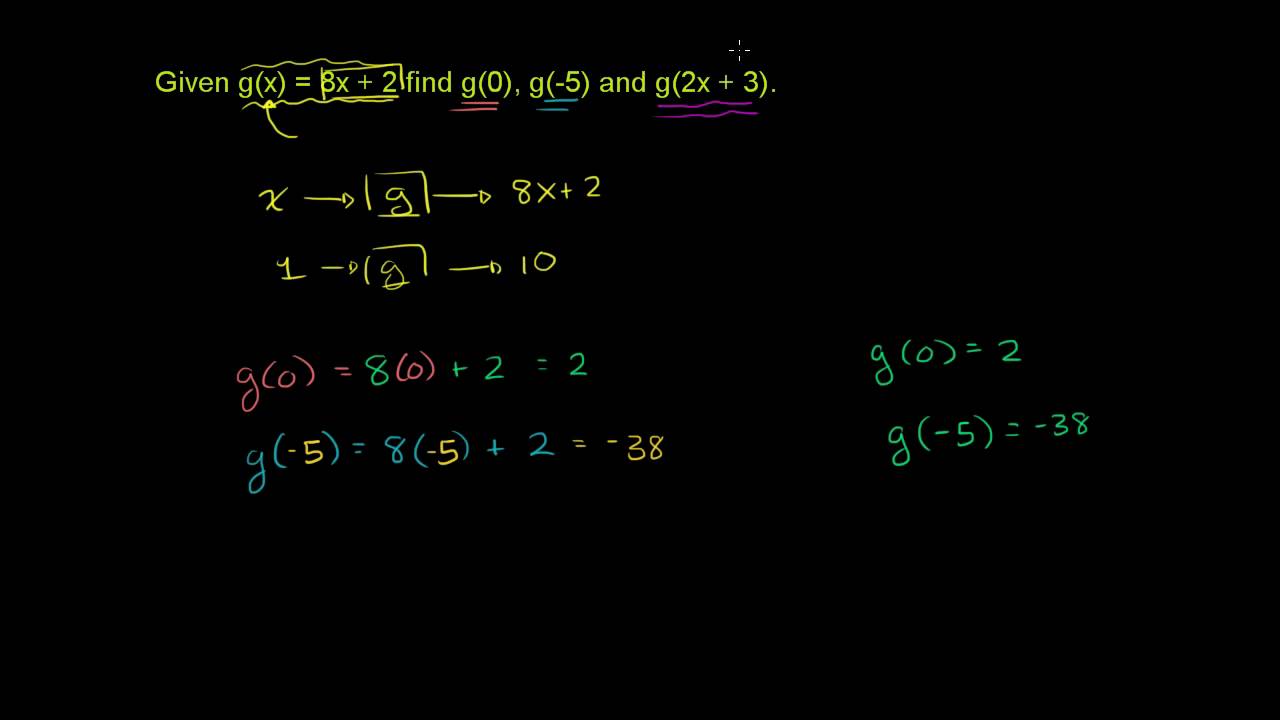
Evaluating Functions