Fourier Reihen Rechtecksimpulsfolge
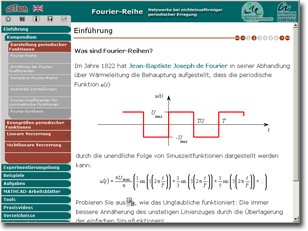
Fourier Reihen Hier werden systematisch und leicht verständlich die koeffizienten der fourier reihe einer 2π periodischen funktion berechnet. 🙏 wir danken für die unterstützung von westermann Österreich. Fourierreihe zu einer rechteckschwingung wir betrachten eine rechteckschwingung mit periode 2 π und sprunghöhe 2 π. für ungerades n lautet die n te fouriernäherung y n (x) = 4 (sin (x) sin (3 x) 3 sin (5 x) 5 sin (n x) n) anhand der graphen beobachten wir eine langsame konvergenz der fouriernäherungen mit wachsendem n. dies spiegelt sich im langsamen abklingen der.
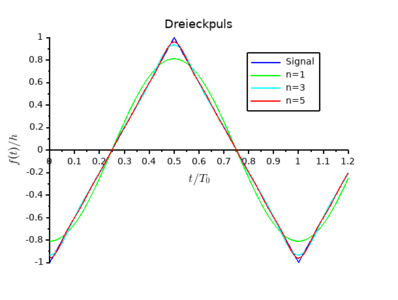
Deprecated Im rahmen der theorie der hilberträume werden auch entwicklungen nach einem beliebigen vollständigen orthonormalsystem als fourierreihe bezeichnet. eine verallgemeinerung ist die fourier transformation. die lehre der fourierreihen ist teil der fourier analyse (klassische harmonische analysis). 2.3 herleitung der fourier reihe 2.3.1 trigonometrische reihe eine trigonometrische reihe ist eine reihe der form Œÿ ak cos(kx) bk sin(kx) k=0 rischen reihe. für k = 0 haben wir cos(0) = 1 und sin(0) = 0, somit können wir den ersten term aus de summe nehmen. damit erhalten wir die form d. Bei der spracherkennung werden die fourier transformation und verwandte transformationen verwendet, um die gesprochenen wörter aus dem audiomaterial wiederherzustellen. im allgemeinen benötigst du die fourier transformation, wenn du die frequenzen in einem signal betrachten musst. 2! originalsignal! sinusförmige komponenten! summieren sich zum originalsignal! annäherung eines rechteckimpulses ! durch 1 5 sinusförmige komponenten!.
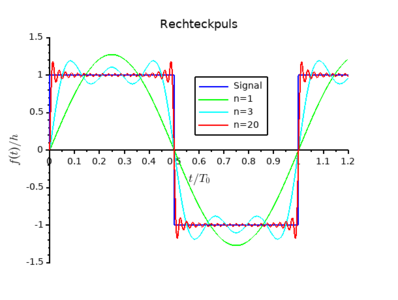
Deprecated Bei der spracherkennung werden die fourier transformation und verwandte transformationen verwendet, um die gesprochenen wörter aus dem audiomaterial wiederherzustellen. im allgemeinen benötigst du die fourier transformation, wenn du die frequenzen in einem signal betrachten musst. 2! originalsignal! sinusförmige komponenten! summieren sich zum originalsignal! annäherung eines rechteckimpulses ! durch 1 5 sinusförmige komponenten!. Fourier reihen: definitionen und beispiele die fourieranalysis beschäftigt sich mit dem problem funktionen in kosinus und sinus zu entwickeln. diese darstellungen sind in der mathematik sowie in der phy sik von großer bedeutung und finden in vielen bereichen anwendung. Die fourier reihe besitzt allgemein die form f (x) = a 0 2 ∑ n = 1 ∞ a n cos (n ω 0 x) b n sin (n ω 0 x) f (x) = 2a0 n=1∑∞ an cos(nω0x) bnsin(nω0x) mit dem periodenintervall l l und der eigenfrequenz ω 0 = 2 π l ω0 = 2π l. da es sich im beispiel um eine 2 π 2π periodische funktion handelt, ist l = 2 π l = 2π und. Vor 200 jahren ̈uberraschte fourier die mathematiker frankreichs mit der behaup tung, dass sich jede funktion s(x ) mit diesen eigenschaften als eine unendliche reihe von sinusfunktionen darstellen l ̈asst. diese idee setzte eine enorme entwick lung der fourier reihen in gang. Einen beweis für diese aussage und das verhalten einer geraden funktion f bei der berechnung der fourier koe zienten wird in den Übungsaufgaben weiter untersucht.
Deprecated Fourier reihen: definitionen und beispiele die fourieranalysis beschäftigt sich mit dem problem funktionen in kosinus und sinus zu entwickeln. diese darstellungen sind in der mathematik sowie in der phy sik von großer bedeutung und finden in vielen bereichen anwendung. Die fourier reihe besitzt allgemein die form f (x) = a 0 2 ∑ n = 1 ∞ a n cos (n ω 0 x) b n sin (n ω 0 x) f (x) = 2a0 n=1∑∞ an cos(nω0x) bnsin(nω0x) mit dem periodenintervall l l und der eigenfrequenz ω 0 = 2 π l ω0 = 2π l. da es sich im beispiel um eine 2 π 2π periodische funktion handelt, ist l = 2 π l = 2π und. Vor 200 jahren ̈uberraschte fourier die mathematiker frankreichs mit der behaup tung, dass sich jede funktion s(x ) mit diesen eigenschaften als eine unendliche reihe von sinusfunktionen darstellen l ̈asst. diese idee setzte eine enorme entwick lung der fourier reihen in gang. Einen beweis für diese aussage und das verhalten einer geraden funktion f bei der berechnung der fourier koe zienten wird in den Übungsaufgaben weiter untersucht.

Solution Fourier Reihe Studypool Vor 200 jahren ̈uberraschte fourier die mathematiker frankreichs mit der behaup tung, dass sich jede funktion s(x ) mit diesen eigenschaften als eine unendliche reihe von sinusfunktionen darstellen l ̈asst. diese idee setzte eine enorme entwick lung der fourier reihen in gang. Einen beweis für diese aussage und das verhalten einer geraden funktion f bei der berechnung der fourier koe zienten wird in den Übungsaufgaben weiter untersucht.
Comments are closed.