If Ab And Ba Then Ab
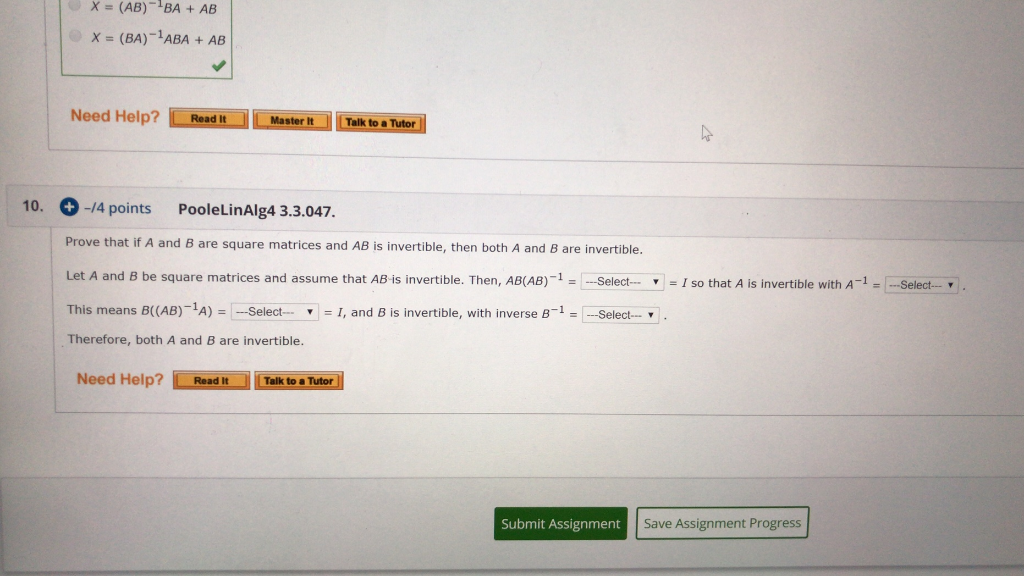
Solved X Ab Ba Ab X Ba Aba Ab Need Help Read It Chegg If $a$ and $b$ are square matrices such that $ab = i$, where $i$ is the identity matrix, show that $ba = i$. i do not understand anything more than the following. In general, ab 6= ba, even if a and b are both square. if ab = ba, then we say that a and b commute. for a general matrix a, we cannot say that ab = ac yields b = c. (however, if we know that a is invertible, then we can multiply both sides of the equation ab = 1 ac to the left by a and get b = c.).

Solved If Possible Find Ab Ba And A 2 If Not Possible Chegg An easy generalization is that if a and b are diagonal and of the same dimensions, then ab=ba; another one is that if a is an m×n matrix and b is an n×m matrix, with m≠n, then ab and ba both exist but are not equal. Hint: to solve this question first we have to understand what is an idempotent matrix. and then we have to start from given and proceed towards checking whether a or b is idempotent. that means on multiplying with itself either it yields the same or not. Example 24 if a and b are symmetric matrixes of the same order, then show that ab is symmetric if and only if a and b commute, that is ab = ba. given a & b are symmetric matrix i.e. a’ = a b’ = b we need to show ab is symmetric if and only if a & b commute (i.e. ab = ba) i. Prove: if ab and ba are both defined, then ab and ba are square matrices. (b) prove: if a is an m times n matrix and a (ba) is defined, then b is an n times m matrix. your solution’s ready to go! our expert help has broken down your problem into an easy to learn solution you can count on.

7 If A Ab Ba 1 And B Ab And Ba Es Example 24 if a and b are symmetric matrixes of the same order, then show that ab is symmetric if and only if a and b commute, that is ab = ba. given a & b are symmetric matrix i.e. a’ = a b’ = b we need to show ab is symmetric if and only if a & b commute (i.e. ab = ba) i. Prove: if ab and ba are both defined, then ab and ba are square matrices. (b) prove: if a is an m times n matrix and a (ba) is defined, then b is an n times m matrix. your solution’s ready to go! our expert help has broken down your problem into an easy to learn solution you can count on. To solve the problem where we have two matrices a and b such that ab =a and ba= b, we will derive some properties of these matrices step by step. step 1: start with the given equations. Given two square matrices a, b a, b with same dimension, what conditions will lead to this result? or what result will this condition lead to? i thought this is a quite simple question, but i can find little information about it. thanks. Let $a, b$ be two matrices such that $ab=a$ and $ba=b$, how do i show that $a\cdot a=a$ and $b\cdot b=b$? steps i took: let $a= \left [\begin {array} {rr} a & b \\ c & d \\ \end {a. Bk 1 = r.h.s hence p (k 1) is true ∴ by the mathematical induction p (n) is true for all n (where n is natural number) hence if ab = ba, then (ab)n = anbn where n ∈ n.
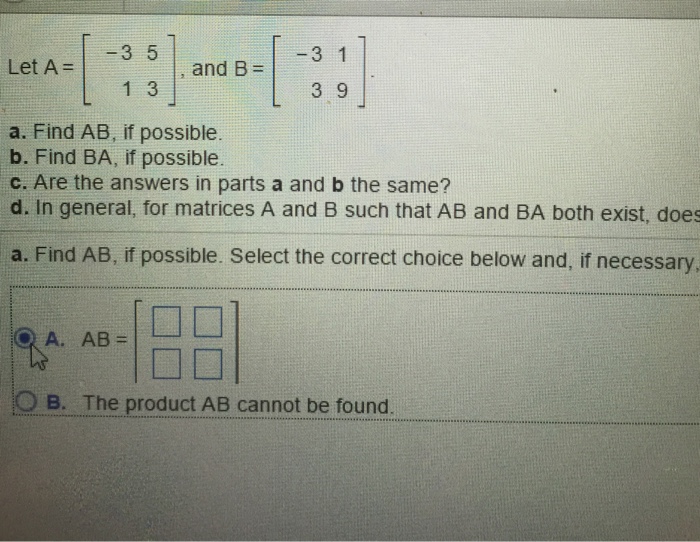
Solved Find Ab If Possible Find Ba If Possible Are The Chegg To solve the problem where we have two matrices a and b such that ab =a and ba= b, we will derive some properties of these matrices step by step. step 1: start with the given equations. Given two square matrices a, b a, b with same dimension, what conditions will lead to this result? or what result will this condition lead to? i thought this is a quite simple question, but i can find little information about it. thanks. Let $a, b$ be two matrices such that $ab=a$ and $ba=b$, how do i show that $a\cdot a=a$ and $b\cdot b=b$? steps i took: let $a= \left [\begin {array} {rr} a & b \\ c & d \\ \end {a. Bk 1 = r.h.s hence p (k 1) is true ∴ by the mathematical induction p (n) is true for all n (where n is natural number) hence if ab = ba, then (ab)n = anbn where n ∈ n.
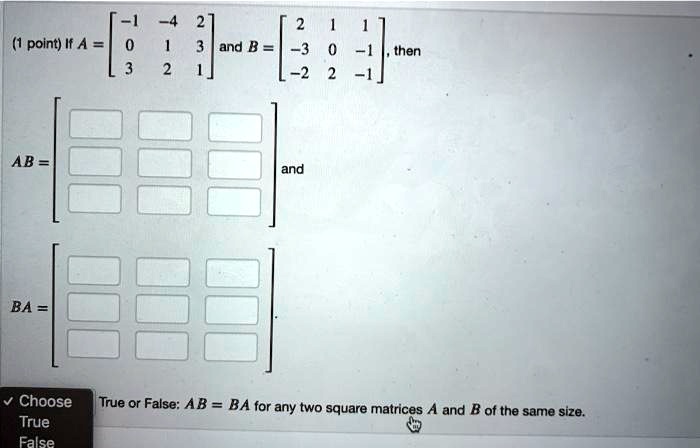
Solved Point If A And B Then Ab And Ba Choose True False True Or False Ab Ba For Let $a, b$ be two matrices such that $ab=a$ and $ba=b$, how do i show that $a\cdot a=a$ and $b\cdot b=b$? steps i took: let $a= \left [\begin {array} {rr} a & b \\ c & d \\ \end {a. Bk 1 = r.h.s hence p (k 1) is true ∴ by the mathematical induction p (n) is true for all n (where n is natural number) hence if ab = ba, then (ab)n = anbn where n ∈ n.
Comments are closed.