Lagrangian Dynamics Pdf Pdf Lagrangian Mechanics Calculus Of Variations

Lagrangian Dynamics PDF | PDF | Lagrangian Mechanics | Calculus Of Variations

Lagrangian Dynamics PDF | PDF | Lagrangian Mechanics | Calculus Of Variations We will derive the equations of motion, i.e. newton’s laws, using a powerful variational principle known as the principle of extremal action, which lies at the foundation of lagrange’s approach to mechanics. These notes are intended as an elementary introduction into these ideas and the basic prescription of lagrangian and hamiltonian mechanics.

Notes Lagrangian Mechanics | PDF

Notes Lagrangian Mechanics | PDF Following this, the book turns to the calculus of variations to derive the euler–lagrange equations. it introduces hamilton’s principle and uses this throughout the book to derive further results. Lagrangian dynamics.pdf free download as pdf file (.pdf), text file (.txt) or read online for free. In this part, we'll finally get to what this book is actually about lagrangian mechanics. we'll be discussing all the basics of lagrangian mechanics and how to use it, including generalized coordinates, generalized momenta and constraints. The real power of lagrangian mechanics is in finding equations of motion for systems with mul tiple degrees of freedom. unlike the energy method, lagrangian mechanics delivers one equation of motion for each coordinate, which is enough to calculate the whole motion of the system.

Lagrangian Dynamics | PDF | Lagrangian Mechanics | Force

Lagrangian Dynamics | PDF | Lagrangian Mechanics | Force In this part, we'll finally get to what this book is actually about lagrangian mechanics. we'll be discussing all the basics of lagrangian mechanics and how to use it, including generalized coordinates, generalized momenta and constraints. The real power of lagrangian mechanics is in finding equations of motion for systems with mul tiple degrees of freedom. unlike the energy method, lagrangian mechanics delivers one equation of motion for each coordinate, which is enough to calculate the whole motion of the system. After discussing the matter of existence of solutions to the euler lagrange equations (a matter which deserves some discussion), we talk about the simplest part of lagrangian dynamics, dynamics near equilibria. Hence, the hamilton's principle and the corresponding euler lagrange equations for the lagrangian (19) are completely equivalent to the netwton's equations of motion in this case. During this term we will be studying two closely connected reformulations of classical mechanics, known as “lagrangian” and “hamiltonian” mechanics. anything that can be doneintheseframeworkscanalsobedoneusingthelanguageofnewtonianmechanics,but thisdoesnotmeanthattheyareuninteresting. The calculus of variations, continued (1) we assume the unknown function f is a continuously differentiable scalar function, and the functional to be minimized depends on y(x) and at most upon its first derivative y0(x).

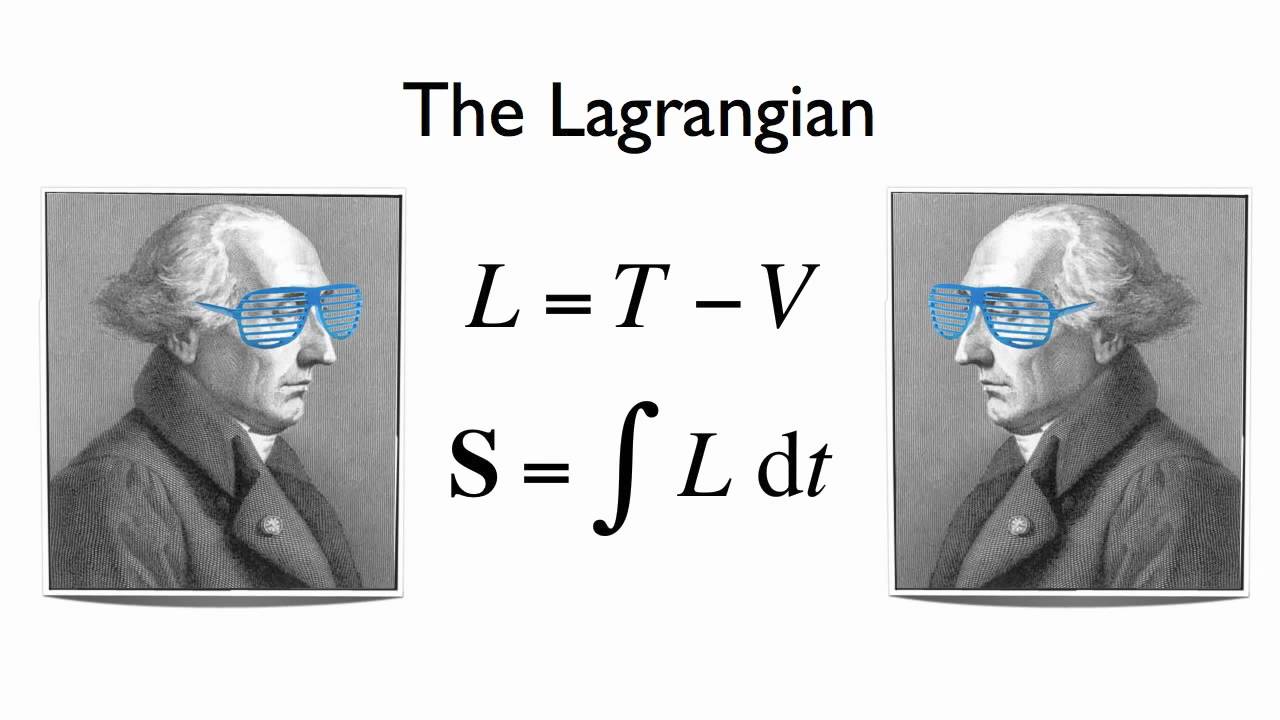
Lagrangian Dynamics