Longest Side Largest Angle Theorem

Solved: 4.5. Longest Side:_ Longest Side: _Shortest Side:_ Shortest Side:_ Largest Angle:_ Lar ...

Solved: 4.5. Longest Side:_ Longest Side: _Shortest Side:_ Shortest Side:_ Largest Angle:_ Lar ... If the smallest side is opposite the smallest angle, and the longest is opposite the largest angle, then it follows that since a triangle only has three sides, the midsize side is opposite the midsize angle. In any non equilateral triangle, the longest side is opposite the largest angle, and vice versa. this theorem holds true for all triangles except equilateral ones.

SOLVED: Arrange The Sides From Shortest To Longest: 2 Arrange The Angles From Largest To ...

SOLVED: Arrange The Sides From Shortest To Longest: 2 Arrange The Angles From Largest To ... This idea is actually a theorem: if one side of a triangle is longer than another side, then the angle opposite the longer side will be larger than the angle opposite the shorter side. This video will how to find the longest and, shortest side given the angles of the triangle and how to find the largest and smallest angle given the side lengths of the triangle .more. In this triangle, we know each angle measure and it is right triangle. the largest angle measure is ∠c. the side which is opposite this angle measure is ab. so, the longest side of the given triangle is ab. list the sides of each triangle in order from shortest to longest. subtracting 89 on both sides. divide by 7 on both sides. This idea is actually a theorem: if one side of a triangle is longer than another side, then the angle opposite the longer side will be larger than the angle opposite the shorter side.

Triangle Larger Angle Theorem

Triangle Larger Angle Theorem In this triangle, we know each angle measure and it is right triangle. the largest angle measure is ∠c. the side which is opposite this angle measure is ab. so, the longest side of the given triangle is ab. list the sides of each triangle in order from shortest to longest. subtracting 89 on both sides. divide by 7 on both sides. This idea is actually a theorem: if one side of a triangle is longer than another side, then the angle opposite the longer side will be larger than the angle opposite the shorter side. Relation between sides and angles in a triangle. theorem in a triangle, the longest side is opposite the largest angle. in other words, the largest angle lies opposite the longest side, the mid sized angle lies opposite the mid sized side, the smallest angle lies opposite the shortest side. theorem on the relation between sides and angles. 1 such result is known as: "the side of a triangle opposite the largest angle is the longest side." you can find its proof in any plane euclidean geometry book. hopefully this helps!. The law of cosines is a generalized version of the pythagorean theorem that applies to all triangles, not just the ones with right angles. according to this law, if a triangle had sides of length a, b and c, and the angle across from the side of length c is c, then c^2 = a^2 b^2 – 2abcosc. In a triangle, the largest angle is across from the longest side. both of these theorems may also be stated using "longer" and " larger" when dealing with 2 sides and 2 angles. ∠ c (across from it) is the largest angle. (across from it) is the longest side.

Solved: 14. In The Triangle Inequality Theorem The Largest Angle Is Opposite The Longest Side ...

Solved: 14. In The Triangle Inequality Theorem The Largest Angle Is Opposite The Longest Side ... Relation between sides and angles in a triangle. theorem in a triangle, the longest side is opposite the largest angle. in other words, the largest angle lies opposite the longest side, the mid sized angle lies opposite the mid sized side, the smallest angle lies opposite the shortest side. theorem on the relation between sides and angles. 1 such result is known as: "the side of a triangle opposite the largest angle is the longest side." you can find its proof in any plane euclidean geometry book. hopefully this helps!. The law of cosines is a generalized version of the pythagorean theorem that applies to all triangles, not just the ones with right angles. according to this law, if a triangle had sides of length a, b and c, and the angle across from the side of length c is c, then c^2 = a^2 b^2 – 2abcosc. In a triangle, the largest angle is across from the longest side. both of these theorems may also be stated using "longer" and " larger" when dealing with 2 sides and 2 angles. ∠ c (across from it) is the largest angle. (across from it) is the longest side.

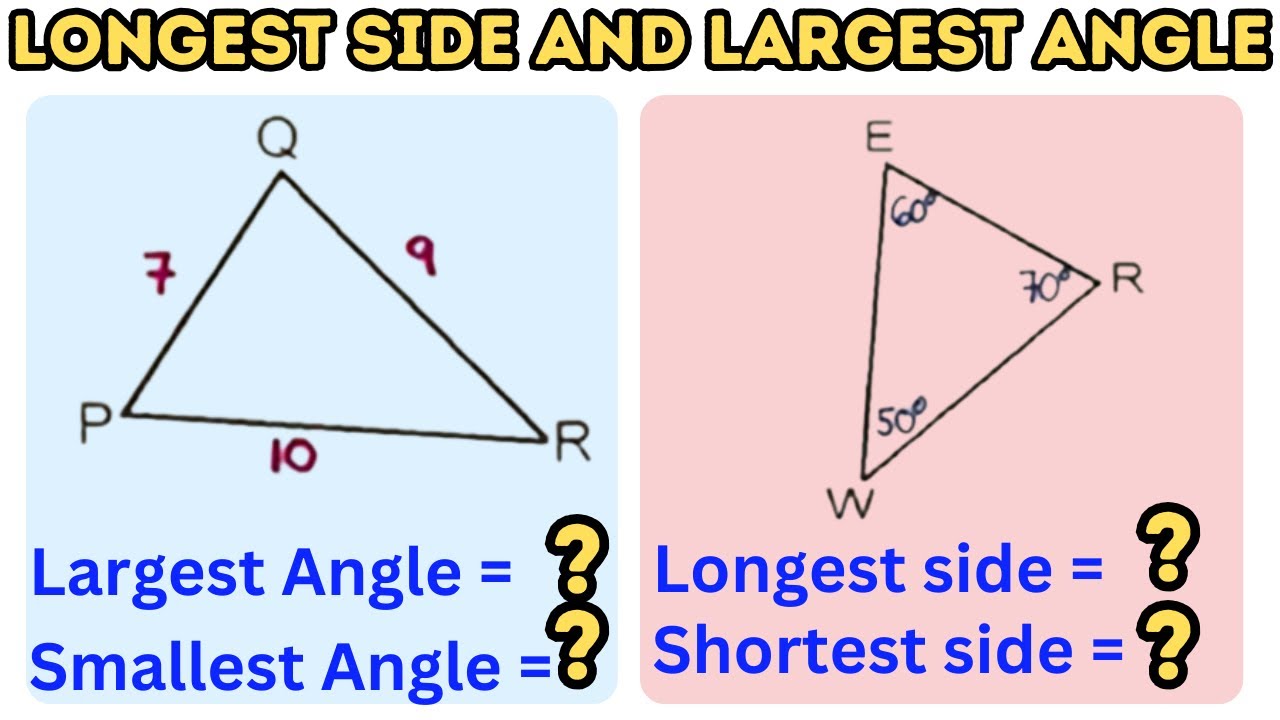
Longest Side, Largest Angle Theorem