Multiplying Matrices

Multiplying Matrices

Multiplying Matrices In linear algebra, the entities that gets multiplied are vectors, the "multiplier" objects are matrices, the operation $\cdot$ generalizes to the matrix vector product, and the operation $\times$ extends to the product between matrices. For large enough matrices, even if you got enough processors to assign one per row, there is still very strong incentive to split multiplied matrices into smaller blocks (but not 1 row or 1 column blocks!) and multiply them using one of the fast multiplication schemes. then just sum the parts and position them in the right places.

Multiplying Matrices

Multiplying Matrices Order of operations for multiplying three matrices ask question asked 7 years, 8 months ago modified 7 years, 8 months ago. Yo, i need some help with understanding matrix multiplication by columns. consider the two matrices: $\\left( \\begin{array}{ccc} 1 & 2 & 3 \\\\ 6 & 5. What is the correct order when multiplying both sides of an equation by matrix inverses? ask question asked 12 years, 1 month ago modified 7 years, 4 months ago. Matrix multiplication is defined so that it works right to left, just like function composition. this allows matrices to represent linear transformations more intuitively. it's also why we conventionally represent vectors as column matrices.

Multiplying Matrices

Multiplying Matrices What is the correct order when multiplying both sides of an equation by matrix inverses? ask question asked 12 years, 1 month ago modified 7 years, 4 months ago. Matrix multiplication is defined so that it works right to left, just like function composition. this allows matrices to represent linear transformations more intuitively. it's also why we conventionally represent vectors as column matrices. The sum of matrices corresponds to the transformation which is the sum of the two given transformations. addition of linear transformations require the domain and range to be identical. the product of matrices corresponds to the transformation which is the composition of the two given transformations. I think this is wrong. you can't partition both of them same way. if you partition after x rows in first matrix , you've to partition after x columns (not rows ) in the second matrix. otherwise while multiplying you'll have to multiply mn block with another mn block which is not possible. (you need np block) try it with your example. Dot product has a specific meaning. matrix multiplication has no specific meaning, than may be a mathematical way to solve system of linear equations why, historically, do we multiply matrices as we do? coming back to dot product algebraically, the dot product is the sum of the products of the corresponding entries of the two sequences of. If the matrices have dimensions that are multiples of each other (or close to multiples) then we can use the square algorithms and block multiplication to speed up the implementation.

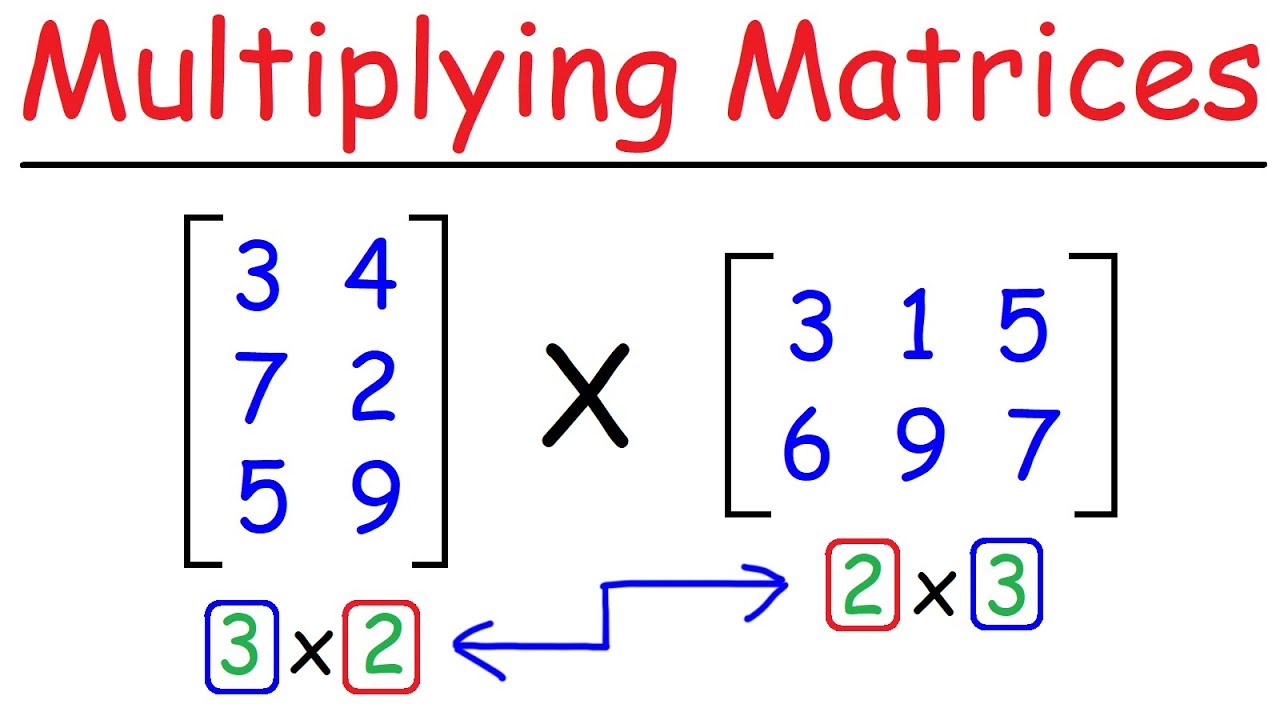
How To Multiply Matrices - Quick & Easy!