Number Theory Modular Arithmetic And Gcd Pdf Ring Theory Mathematical Concepts

Modular Arithmetic Part 1 PDF | PDF

Modular Arithmetic Part 1 PDF | PDF This document discusses modular arithmetic and greatest common divisors (gcds). it begins with definitions of modular arithmetic, including that a ≡ b (mod m) means a b is divisible by m. Can use euclid’s algorithm to find gcd and inverses. polynomials with coefficients in gf(2n) also form a field.

L-5. Modular Arithmetic | PDF | Ring Theory | Mathematics

L-5. Modular Arithmetic | PDF | Ring Theory | Mathematics Proof. recall that an integral domain is a commutative ring a with 1 having no zero divisors, ie xy = 0 =) x = 0 or y = 0: in particular, a eld is an integral domain in which every non zero element has a multiplicative inverse. We begin with integer arithmetic, proving the division theorem, and de ning greatest common divisors and relative primeness. we move onto the de nitions of a ring and eld, and then establish the system of modular arithmetic. Fact: gcd(m; n) is the largest number in divisors(m; n), the smallest number in sums(m; n), and the only number in both. the euclidean algorithm for computing gcd systematically nds smaller and smaller numbers in sums(m; n) until it nds one that is also in divisors(m; n). Introduction to modular arithmetic 1 introduction y speaking is the study of integers and their properties. modular arithmetic highlights the power of remainders when solving problems. in this lecture, i will quickly go over the basics of the subjec.

110BH. Ring-Module Theory Topics (Gim) PDF | PDF | Ring (Mathematics) | Module (Mathematics)

110BH. Ring-Module Theory Topics (Gim) PDF | PDF | Ring (Mathematics) | Module (Mathematics) Fact: gcd(m; n) is the largest number in divisors(m; n), the smallest number in sums(m; n), and the only number in both. the euclidean algorithm for computing gcd systematically nds smaller and smaller numbers in sums(m; n) until it nds one that is also in divisors(m; n). Introduction to modular arithmetic 1 introduction y speaking is the study of integers and their properties. modular arithmetic highlights the power of remainders when solving problems. in this lecture, i will quickly go over the basics of the subjec. Gcd b is the greatest integer that divides both a and b one of the most commonly used tools in solving number theory problems. The chinese remainder theorem says that provided n and m are relatively prime, x has a unique residue class modulo the product nm. that is if we divide our number of beer bottles by 42 = 3 14, then there must be 22 bottles leftover (it's easy to check 22 8 (mod 14) and 22 1 (mod 3)). The study of the properties of the system of remainders is called modular arithmetic. it is an essential tool in number theory. 2.1. definition of z/nz in this section we give a careful treatment of the system called the integers modulo (or mod) n. 2.1.1 definition let a, b ∈ z and let n ∈ n. Lemma 8.9. if r is a ring r⇤ is a group with respect to multiplication. this will be proven in the exercises. the group of invertible elements are easy to determine for the previous examples. for example, mnn(r)⇤ = gln(r). given two integers a, b, a common divisor is an integer d such that and d|b.

Mathematical Rings | PDF | Ring (Mathematics) | Multiplication

Mathematical Rings | PDF | Ring (Mathematics) | Multiplication Gcd b is the greatest integer that divides both a and b one of the most commonly used tools in solving number theory problems. The chinese remainder theorem says that provided n and m are relatively prime, x has a unique residue class modulo the product nm. that is if we divide our number of beer bottles by 42 = 3 14, then there must be 22 bottles leftover (it's easy to check 22 8 (mod 14) and 22 1 (mod 3)). The study of the properties of the system of remainders is called modular arithmetic. it is an essential tool in number theory. 2.1. definition of z/nz in this section we give a careful treatment of the system called the integers modulo (or mod) n. 2.1.1 definition let a, b ∈ z and let n ∈ n. Lemma 8.9. if r is a ring r⇤ is a group with respect to multiplication. this will be proven in the exercises. the group of invertible elements are easy to determine for the previous examples. for example, mnn(r)⇤ = gln(r). given two integers a, b, a common divisor is an integer d such that and d|b.

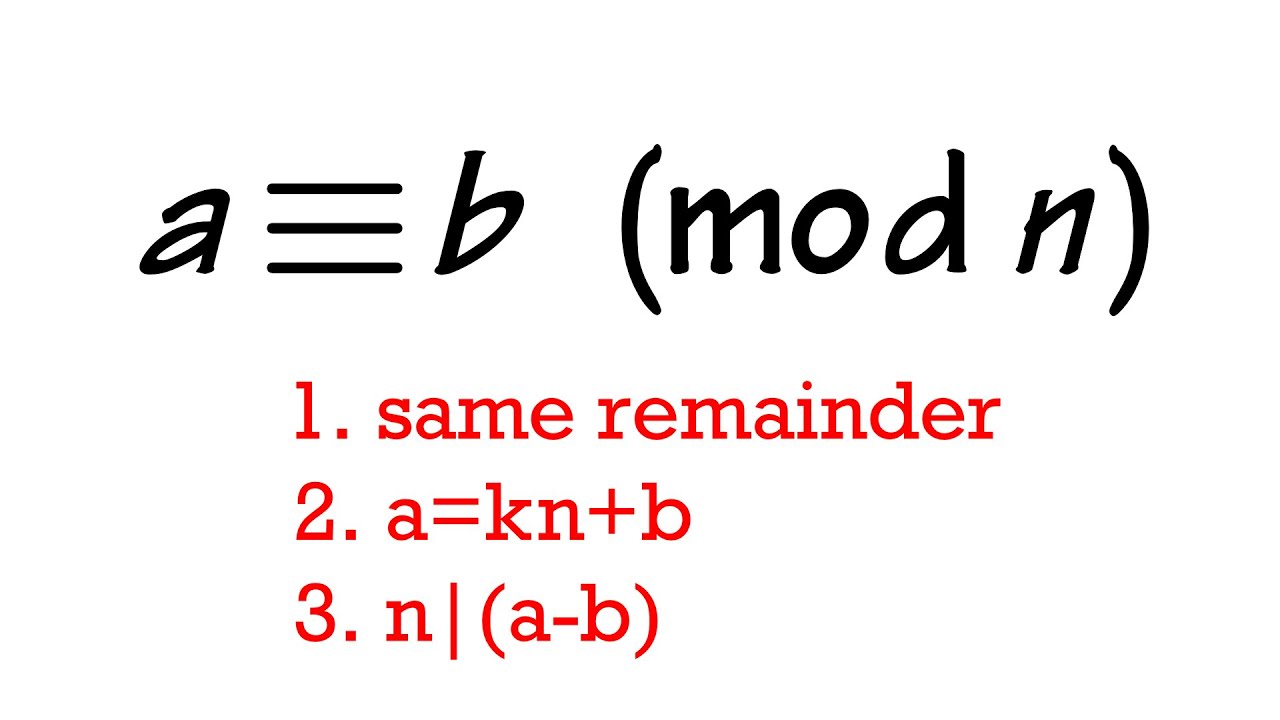
What does a ≡ b (mod n) mean? Basic Modular Arithmetic, Congruence