Set Operations Union Intersection Difference Complement Venn Diagram Maths Sets Unions

Venn Diagram Union Intersection Complement

Venn Diagram Union Intersection Complement The most common set operations, such as union, intersection, disjoint, set difference, etc., will be explored in detail below, including their definitions, examples, and venn diagrams. We denote a set using a capital letter and we define the items within the set using curly brackets. for example, suppose we have some set called “a” with elements 1, 2, 3. we would write this as: a = {1, 2, 3} this tutorial explains the most common set operations used in probability and statistics.

Union Intersection Complement Venn Diagram

Union Intersection Complement Venn Diagram What are the set operations in mathematics. learn its symbols, properties, and venn diagrams with examples. There are four main set operations which include set union, set intersection, set complement, and set difference. in this article, we will learn the various set operations, notations of representing sets, how to operate on sets, and their usage in real life. what are set operations? a set is defined as a collection of objects. The complement of a set $a$, denoted by $a^c$ or $\bar {a}$, is the set of all elements that are in the universal set $s$ but are not in $a$. in figure 1.7, $\bar {a}$ is shown by the shaded area using a venn diagram. Learn how to combine and manipulate sets using operations and visualize them with venn diagrams. this section covers union of sets, intersection of sets, difference of sets, complement of a set, and using venn diagrams to represent these set operations effectively in the sets, relations & functions course.

Exploring The Relationship Between Sets With Venn Diagrams

Exploring The Relationship Between Sets With Venn Diagrams The complement of a set $a$, denoted by $a^c$ or $\bar {a}$, is the set of all elements that are in the universal set $s$ but are not in $a$. in figure 1.7, $\bar {a}$ is shown by the shaded area using a venn diagram. Learn how to combine and manipulate sets using operations and visualize them with venn diagrams. this section covers union of sets, intersection of sets, difference of sets, complement of a set, and using venn diagrams to represent these set operations effectively in the sets, relations & functions course. Learn set operations in maths with clear explanations, venn diagrams, and solved examples. master union, intersection, difference, and complement to solve set questions easily. The following figures give the set operations and venn diagrams for complement, subset, intersection, and union. scroll down the page for more examples and solutions. Sets are fundamental in mathematics and are collections of distinct objects, considered as a whole. in this topic, we will explore the basic operations you can perform on sets, such as union, intersection, difference, and complement. In discrete mathematics, to represent discrete elements as collections, we can use sets. sets are very useful in organizing and structuring the data. when working on sets, we must understand how to perform set operations.

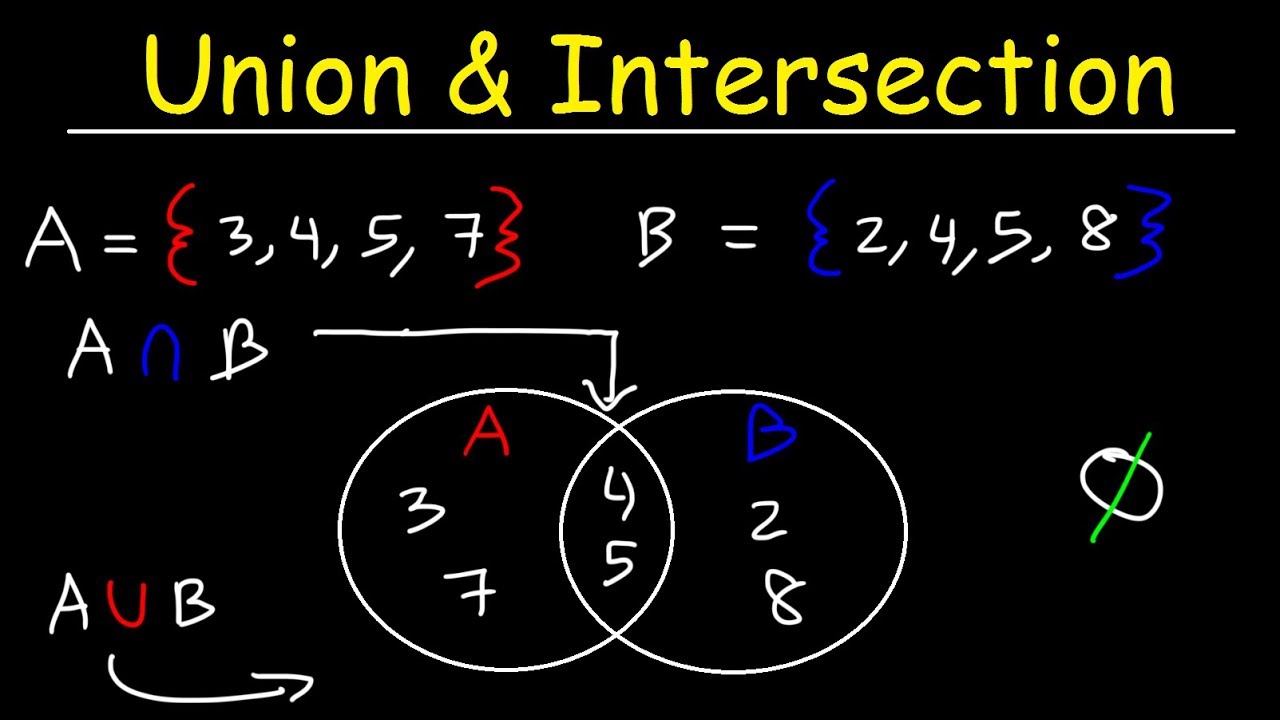
Intersection of Sets, Union of Sets and Venn Diagrams