Set Theory Union And Intersection

Set Theory - Union And Intersection

Set Theory - Union And Intersection The symmetric difference between two sets \ (a\) and \ (b\), denoted by \ (a \bigtriangleup b\), is the set of elements that can be found in \ (a\) and in \ (b\), but not in both \ (a\) and \ (b\). In mathematics, the algebra of sets, not to be confused with the mathematical structure of an algebra of sets, defines the properties and laws of sets, the set theoretic operations of union, intersection, and complementation and the relations of set equality and set inclusion.

Set Theory - Union And Intersection

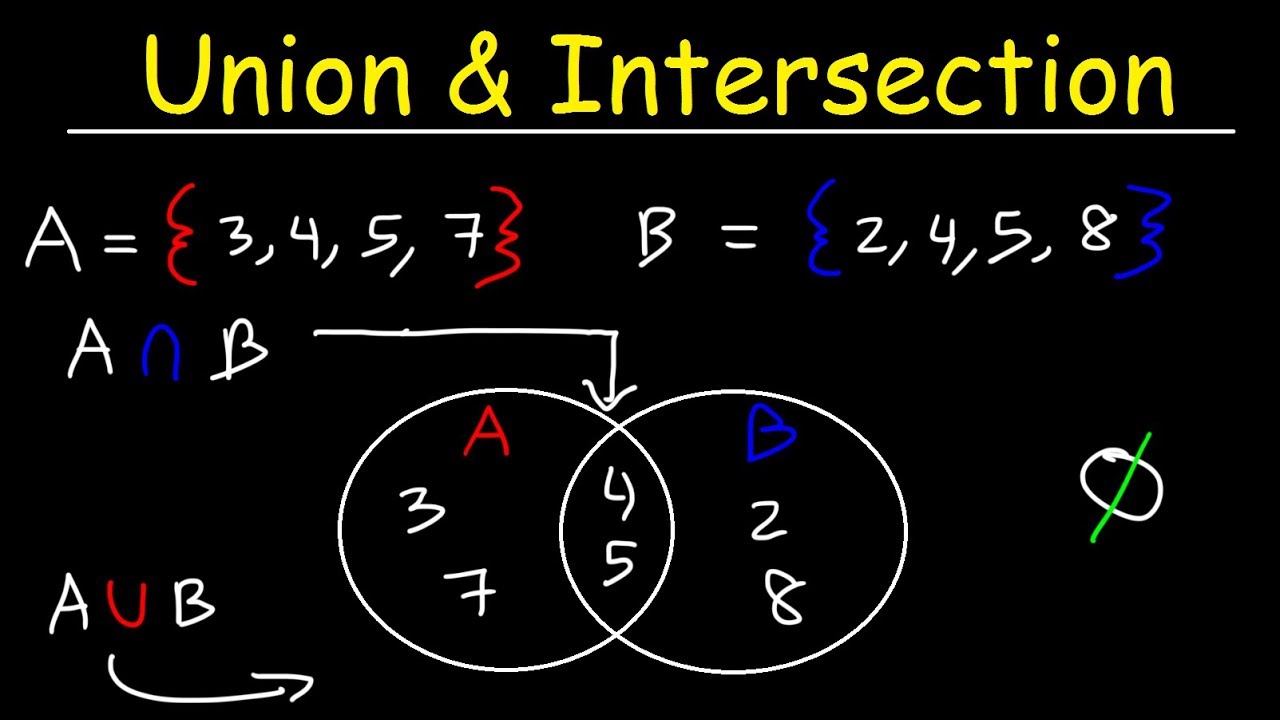
Set Theory - Union And Intersection The most common set operations, such as union, intersection, disjoint, set difference, etc., will be explored in detail below, including their definitions, examples, and venn diagrams. To find the intersection of two or more sets, you look for elements that are contained in all of the sets. to find the union of two or more sets, you combine all the elements from each set together, making sure to remove any duplicates. created by sal khan. want to join the conversation? posted 12 years ago. We denote a set using a capital letter and we define the items within the set using curly brackets. for example, suppose we have some set called “a” with elements 1, 2, 3. we would write this as: a = {1, 2, 3} this tutorial explains the most common set operations used in probability and statistics. In sets and set theory, two of the most fundamental concepts are set union and set intersection. these two concepts build the foundation of sets and give birth to the pictorial representation of sets in venn diagrams.

Set Theory - Union And Intersection | PPT

Set Theory - Union And Intersection | PPT We denote a set using a capital letter and we define the items within the set using curly brackets. for example, suppose we have some set called “a” with elements 1, 2, 3. we would write this as: a = {1, 2, 3} this tutorial explains the most common set operations used in probability and statistics. In sets and set theory, two of the most fundamental concepts are set union and set intersection. these two concepts build the foundation of sets and give birth to the pictorial representation of sets in venn diagrams. Master set operations with our ultimate guide to union and intersection of sets. learn clear definitions, practical examples, and step by step visual explanations to boost your math skills. Method 1: roster notation: a roster is a list of the elements in a set, separated by commas and surrounded by french curly braces. Sets are useful in many areas of mathematics, such as comparing groups, understanding data, and solving problems using venn diagrams and operations like union and intersection. the concept of sets allows us to define relationships between objects and perform operations on sets. If two sets a and b are given, then the intersection of a and b is the subset of universal set u, which consist of elements common to both a and b. it is denoted by the symbol ‘∩’. this operation is represented by: a∩b = {x : x ∈ a and x ∈ b} where x is the common element of both sets a and b.

Set Theory (Union, Intersection) Notes By Overflow Technologies | TPT

Set Theory (Union, Intersection) Notes By Overflow Technologies | TPT Master set operations with our ultimate guide to union and intersection of sets. learn clear definitions, practical examples, and step by step visual explanations to boost your math skills. Method 1: roster notation: a roster is a list of the elements in a set, separated by commas and surrounded by french curly braces. Sets are useful in many areas of mathematics, such as comparing groups, understanding data, and solving problems using venn diagrams and operations like union and intersection. the concept of sets allows us to define relationships between objects and perform operations on sets. If two sets a and b are given, then the intersection of a and b is the subset of universal set u, which consist of elements common to both a and b. it is denoted by the symbol ‘∩’. this operation is represented by: a∩b = {x : x ∈ a and x ∈ b} where x is the common element of both sets a and b.

Intersection Set Theory Union Universal Set, PNG, 899x1024px, Intersection, Algebra, Algebra Of ...

Intersection Set Theory Union Universal Set, PNG, 899x1024px, Intersection, Algebra, Algebra Of ... Sets are useful in many areas of mathematics, such as comparing groups, understanding data, and solving problems using venn diagrams and operations like union and intersection. the concept of sets allows us to define relationships between objects and perform operations on sets. If two sets a and b are given, then the intersection of a and b is the subset of universal set u, which consist of elements common to both a and b. it is denoted by the symbol ‘∩’. this operation is represented by: a∩b = {x : x ∈ a and x ∈ b} where x is the common element of both sets a and b.

Intersection of Sets, Union of Sets and Venn Diagrams