Solve The Following Initial Value Problem Part A

Solved Solve The Following Initial Value Problem Chegg Our expert help has broken down your problem into an easy to learn solution you can count on. = ec and add 5 to both sides to solve for y. y(t) 2t = 5 ae apply the initial condition now to determine a. a = y0 therefore, y(t) = 5 (y0 5)e 2t:.

Solved Solve The Following Initial Value Problem Chegg Solve the following initial value problem and find the interval on which the solution is defined (part a). please subscribe and give the video a thumps up!. Goals the goal of this section is to use laplace transform to solve initial value problems, second order linear equations (as in §3.1, 3.3, 3.4, 3.5, 3.6). this way, the methods may become more algebraic. two theorem that follows would be instrumental for this method. Here we turn to one common use for antiderivatives that arises often in many applications: solving differential equations. a differential equation is an equation that relates an unknown function and one or more of its derivatives. Problems the elementary theory of initial value. use theorem 5.4 to show that the following initial value problem has a unique solution, and find the solution. solution. 1, ≤ t ≤ 0 y(0) = 1. a.
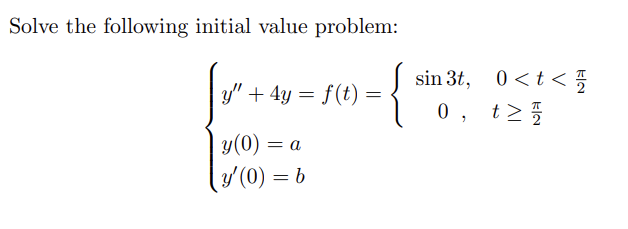
Solved Solve The Following Initial Value Problem Chegg Here we turn to one common use for antiderivatives that arises often in many applications: solving differential equations. a differential equation is an equation that relates an unknown function and one or more of its derivatives. Problems the elementary theory of initial value. use theorem 5.4 to show that the following initial value problem has a unique solution, and find the solution. solution. 1, ≤ t ≤ 0 y(0) = 1. a. Thus, the initial value problem has a unique solution for a · t · b. we now solve the initial value problem. thus, dy 4t3y. Question: 3. solve the following differential equations or initial value problems. in part (a), leave your answer in implicit form. for parts (b) and (c), write your answer in explicit form. 2 7 (a) y = x (b) y' = (cosa y) int (c) (t2 t) y y2 = ty?, y (1) = 1 y4 – 4y3; y (1) = 2. Suppose d = [a; b] r, a function f is continuous on d and lipschitz with respect to y, then the initial value problem y0 = f (t; y) for t 2 [a; b] with initial value y(a) = has a unique solution y(t) for t 2 [a; b]. Find the time that must elapse for the object to reach 98% of its limiting velocity. how far does the object fall in the time found in part (a)? start by solving the initial value problem. note that t is measured in seconds, and the velocity is measured in meters=second. 49.
Comments are closed.