Solving Trigonometry How Far Did A Ship Travel Based On Course Hero

301 Moved Permanently

301 Moved Permanently Two of the angles in the triangle are known from the bearings, and one side of the triangle is equal to the distance from the ship to the lighthouse at the bearing ne. 37.9° a diagram containing the information is shown on the right. To be able to solve these problems it is important that you have a grasp of the major trigonometric identities, the pythagoras rule, the sine rule and the cosine rule.

Understanding Spherical Trigonometry: Key Problems And Solutions | Course Hero

Understanding Spherical Trigonometry: Key Problems And Solutions | Course Hero Now, let's look at a problem where we find the distance using right triangles as bearings. a ship travels on a n 50 ∘ e course. the ship travels until it is due north of a port which is 10 nautical miles due east of the port from which the ship originated. how far did the ship travel?. Question 1120575: a ship travels on a n 34o e course. the ship travels until it is due north of a port which is 245 nm due east of the port from which the ship originated. how far did the ship travel? round your answer to two decimal places. answer by ankor@dixie net.com (22740) (show source):. A ship is 4 degrees off course. if the ship is traveling at 10 miles per hour, how far off course will it be after 6 hours. In the first question, the ship travels on a n50e course. this means the ship is traveling at an **angle **of 50 degrees east of north. to find how far the ship traveled, we can use trigonometry. we can use the sine function, sine (angle) = opposite/hypotenuse, to find the distance traveled north.

[Solved] Trigonometry. X Ship A Is 50 Km From X On A Bearing Of 2580. Ship B... | Course Hero

[Solved] Trigonometry. X Ship A Is 50 Km From X On A Bearing Of 2580. Ship B... | Course Hero A ship is 4 degrees off course. if the ship is traveling at 10 miles per hour, how far off course will it be after 6 hours. In the first question, the ship travels on a n50e course. this means the ship is traveling at an **angle **of 50 degrees east of north. to find how far the ship traveled, we can use trigonometry. we can use the sine function, sine (angle) = opposite/hypotenuse, to find the distance traveled north. In this scenario, after determining the positions of the ships, we can use this law to calculate the distance between them by treating their paths as the sides of a triangle. this concept is essential for solving problems involving non right triangles in trigonometry. To compensate for an easterly current, he aims for a point on shore that is 5 km west of port harbour. assuming that the point on shore is 20 km from his position now,. How high above the ground is the penguin? example 4: using trig in navigation a u.s. coast guard patrol boat leaves port cleveland and averages 35 knots (nautical mph) traveling for and then 3 hours on a course of 143°. what s the boat’s bear. **3. use trigonometry** we need to find the distance p1s, which is the distance the ship traveled. * we have angle sp1p2 = 62°, and we know the adjacent side (p1p2 = 200 nm). * we need to find the hypotenuse (p1s). * we can use the cosine function: cos (angle) = adjacent / hypotenuse * cos (62°) = p1p2 / p1s * cos (62°) = 200 / p1s **4.

[Solved] Trigonometry. X Ship A Is 50 Km From X On A Bearing Of 2580. Ship B... | Course Hero

[Solved] Trigonometry. X Ship A Is 50 Km From X On A Bearing Of 2580. Ship B... | Course Hero In this scenario, after determining the positions of the ships, we can use this law to calculate the distance between them by treating their paths as the sides of a triangle. this concept is essential for solving problems involving non right triangles in trigonometry. To compensate for an easterly current, he aims for a point on shore that is 5 km west of port harbour. assuming that the point on shore is 20 km from his position now,. How high above the ground is the penguin? example 4: using trig in navigation a u.s. coast guard patrol boat leaves port cleveland and averages 35 knots (nautical mph) traveling for and then 3 hours on a course of 143°. what s the boat’s bear. **3. use trigonometry** we need to find the distance p1s, which is the distance the ship traveled. * we have angle sp1p2 = 62°, and we know the adjacent side (p1p2 = 200 nm). * we need to find the hypotenuse (p1s). * we can use the cosine function: cos (angle) = adjacent / hypotenuse * cos (62°) = p1p2 / p1s * cos (62°) = 200 / p1s **4.

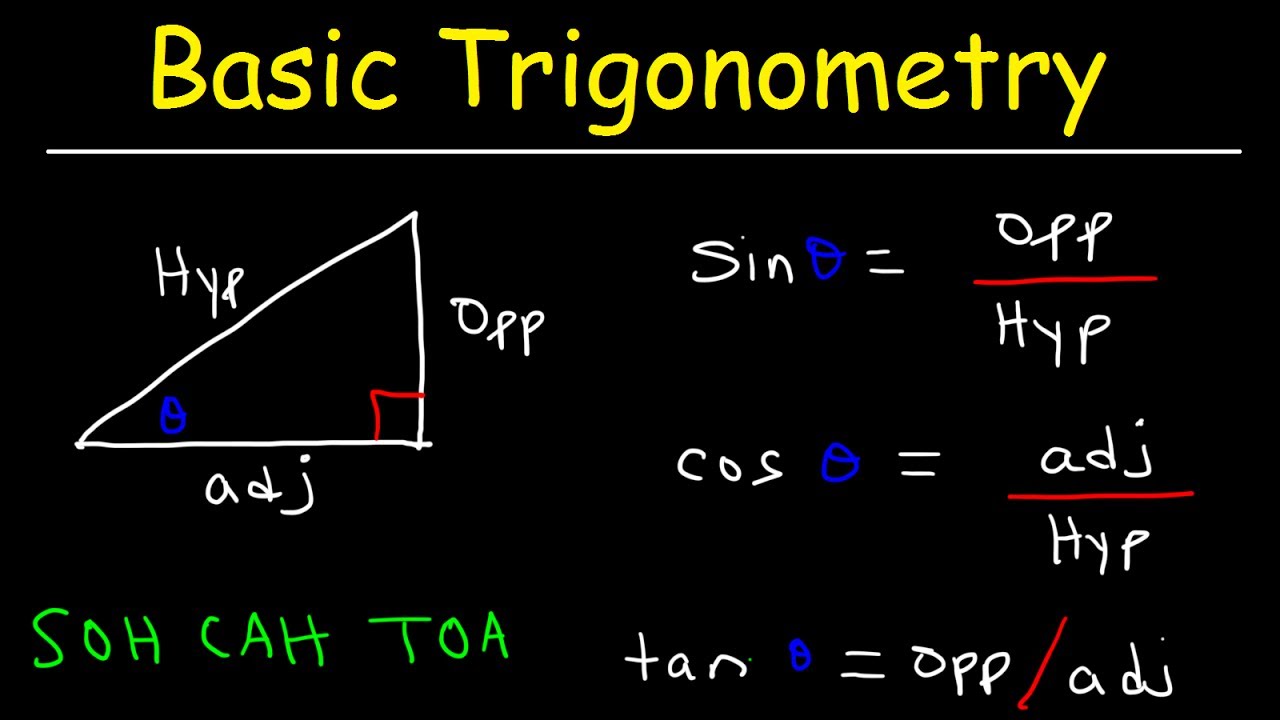
Trigonometry For Beginners!